Ever wondered what happens when you try to write one third as a regular decimal number? It’s a little trickier than converting one half (0.5) or one quarter (0.25), and it involves a concept called a repeating decimal. Lets explore this curious number together!
Understanding fractions and decimals is super useful in everyday life, from splitting a pizza with friends to measuring ingredients for a baking recipe. So, grab your thinking cap, and let’s dive into the world of one third and its decimal form. It’s easier than you might think!
Unlocking the Mystery
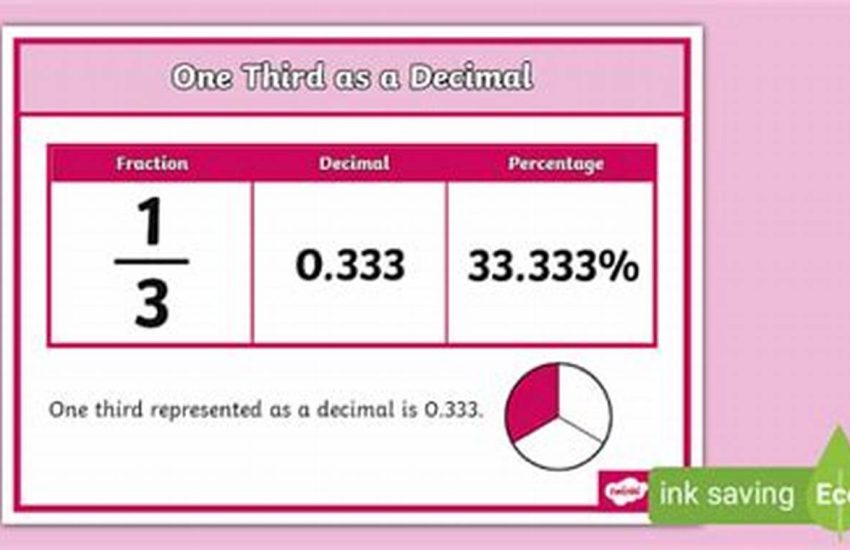
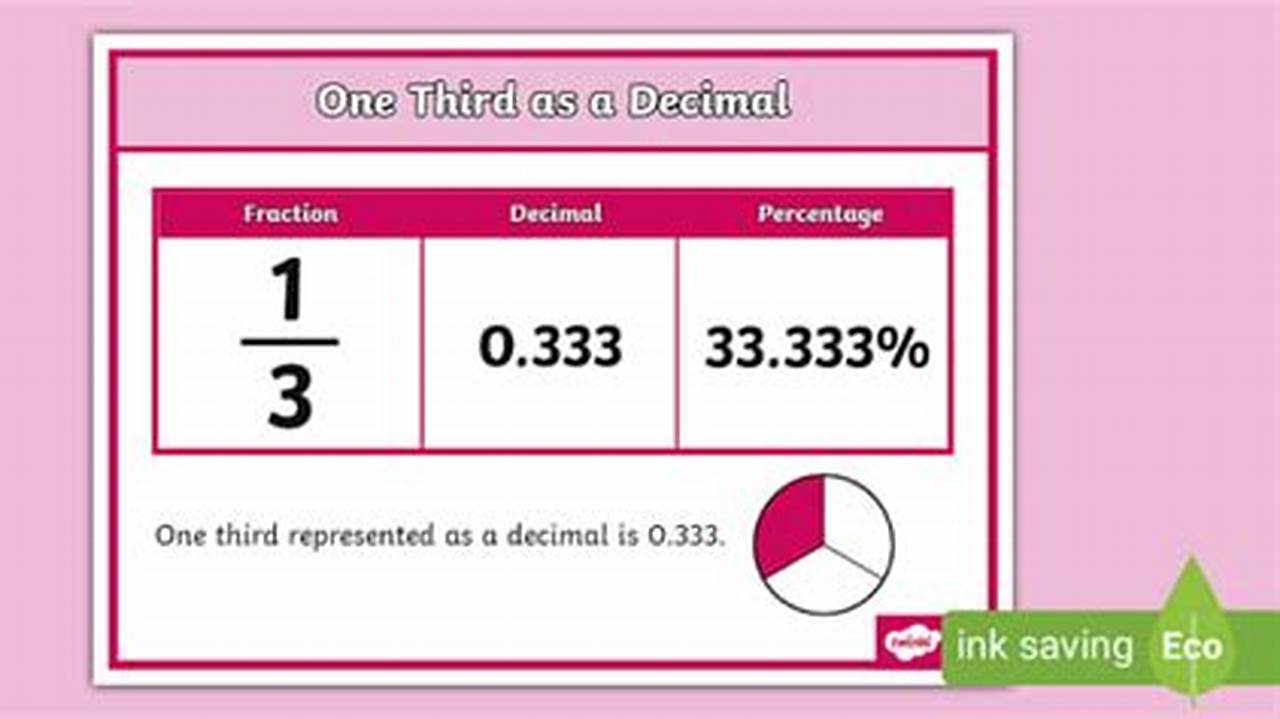
So, what is one third in decimal form? When you divide 1 by 3, you get 0.333… The three dots (…) mean that the 3s go on forever, repeating endlessly. This type of decimal is called a repeating decimal, and it’s how we represent fractions that don’t have a clean, finite decimal equivalent.
Instead of writing out a never-ending string of 3s, we use a shorthand. We write 0.3 with a line over the 3 (0.3). The line, called a vinculum, indicates that the digit underneath repeats infinitely. This is the accurate and concise way to represent one third in decimal form.
Why does this happen? Fractions like one third don’t fit neatly into our base-ten number system. Decimals are based on powers of ten (tenths, hundredths, thousandths, etc.). Because 3 isn’t a factor of 10, we can’t find a decimal that perfectly represents one third in a finite number of digits.
When you use one third in decimal form in calculations, remember that 0.333… is just an approximation. Depending on the level of precision you need, you might use 0.33 or 0.333. However, for exact calculations, its best to stick with the fraction 1/3.
Consider a recipe that calls for one third of a cup of flour. While you could try to measure out 0.33 cups, it’s much easier and more accurate to use a one-third measuring cup! This highlights how both fractions and decimals have their place in our daily lives, each serving a unique purpose.
Now that you understand one third in decimal form, you’re ready to tackle other repeating decimals. Practice converting different fractions into decimals and see which ones repeat. It’s a fun and engaging way to sharpen your math skills and understand the relationship between fractions and decimals!